- 자연수의 집합 $ S = {1, 2, ..., n} $에 대하여 $ S $에서 $ S $로의 일대일 대응 함수를 치환(permutation)이라 한다.
쉽게 말해 1부터 $ n $까지의 수를 임의의 순서로 나열한 것(순열)이다. - 치환 $ \sigma = <j_{1}, j_{2}, ..., j_{n}> $은 다음과 같이 큰 수가 작은 수보다 앞에 오는 경우를 반전(inversion)이 일어났다고 한다. $ j_{s}>j_{t}, s<t $.
예를 들어 치환 $ \sigma =<3, 1, 5, 4, 2> $에서 3은 1, 2보다 앞서고, 5는 4, 2보다 앞서고, 4는 2보다 앞서므로 반전이 총 5번 일어났다고 한다. - 어떤 치환에 대하여 반전수가 짝수이면 짝치환(even permutation), 홀수이면 홀치환(odd permutation)이라고 하며 $ S_{n} $의 한 치환 $ \sigma $의 부호(sign)을 다음과 같이 정의한다.

$ k $는 $ \sigma $의 반전수이다.
- 모든 $ n\times n $행렬에 대하여 함수 $ f:M_{n\times n}(\mathbb{R})\to \mathbb{R} $가 다음 세 조건을 만족하는 경우 행렬식(determinant)라고 정의한다.
(1) 행렬이 단위행렬일 때 $ f $의 값은 1이다. $ f(I_{n})=1 $
(2) 어떠한 두 행의 위치가 바뀌면 $ f $의 값은 부호가 바뀐다.
(3) $ f $는 첫 행에서 선형성(linearity)을 갖는다. 임의의 실수 $ k, l $에 대하여 $ f\begin{bmatrix}
k\textbf{r}_{1}+l\textbf{r}_{1}'\\
\textbf{r}_{2}\\
\vdots\\
\textbf{r}_{n}
\end{bmatrix}
=kf\begin{bmatrix}
\textbf{r}_{1} \\
\textbf{r}_{2} \\
\vdots\\
\textbf{r}_{n}\end{bmatrix}+lf\begin{bmatrix}
\textbf{r}_{1}' \\
\textbf{r}_{2}\\
\vdots\\
\textbf{r}_{n}\end{bmatrix} $이 성립한다. $ \textbf{r}_{i} $는 행렬의 열벡터를 나타낸다.
$ A $의 행렬식(determinant)은 $ det A $또는 $ |A| $로 나타낸다. - 행렬식의 성질 1
(1) 행렬식은 모든 행에서 선형성(linearity)을 갖는다
(2) 행렬 $ A $의 한 행이 0이거나 두 개의 행이 서로 같으면 $ det A=0 $이다.
(3) 행렬에서 한 행의 상수배를 다른 행에 더하는 기본행 연산의 결과는 행렬식의 값에 영향을 주지 않는다.
(4) $ E $를 기본행렬이라고 하면, $ det A \neq 0 $이다.
(5) $ det(EA)=det E det A $이다.
(6) 행렬 $ B $가 행렬 $ A $의 두 행을 서로 바꾼 행렬이면 $ det B = -det A $이다.
(7) 삼각행렬의 determinant 값은 주대각성분들의 곱이다.
(8) 행렬 $ A $가 가역(invertible)행렬일 필요충분조건은 $ det A \neq 0 $이고, $ det A^{-1} = \frac{1}{det A} $이다.
(9) $ det A^T=det A $이다. 따라서 행들에 관한 성질들이 열에서도 적용된다. - 행렬식 구하기 1. Leibniz formula(라이프니츠 공식)
$ n\times n $행렬 $ A $에 대하여, $ det A=\sum_{\sigma \in S_{n}}^{}sign(\sigma)a_{1\sigma (1)}a_{2\sigma (2)}\cdots a_{n\sigma (n)} $ 즉, 각 치환의 원소들과 부호의 원소를 곱한 것을 더한 것이다. - 행렬식 구하기 2. Sarrus' Method(사루스 공식)
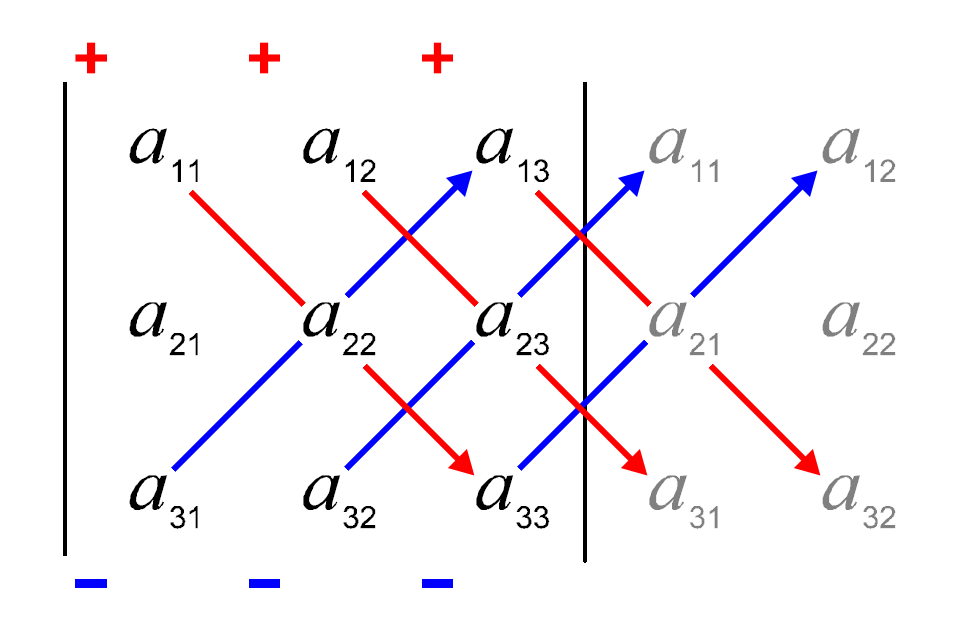
3차 이하의 행렬식에서만 성립한다. 오른쪽 아래 방향 대각선 성분들을 모두 곱하고 부호가 +이며 왼쪽 아래 방향 대각선 성분들은 모두 곱하고 부호가 -이다. 행렬식의 성질들(특히(3))을 이용하여 행렬을 간단하게 만든 후 공식으로 행렬식을 구하면 계산을 훨씬 더 간단하게 만들 수 있다.
'Mathematics > 선형대수(Linear Algebra)' 카테고리의 다른 글
| Chapter 3-1. 부분 공간과 일차 독립 (0) | 2022.05.26 |
|---|---|
| Chapter 2-2. 여인자 전개와 크래머 공식 (0) | 2022.05.26 |
| Chapter 1-3 역행렬과 선형연립방정식의 해 구하기 (0) | 2022.05.24 |
| Chapter 1 - 2. 행렬의 덧셈과 곱셈 (0) | 2022.05.24 |
| Chapter 1-1. 선형연립방정식과 Gauss-Jordan 소거법 (0) | 2022.05.24 |