- $ m\times n $ 행렬(matrix)은 $ m $개의 행(rows)과 $ n $개의 열(column)으로 이루어져 있으며 다음과 같이 나타낸다.
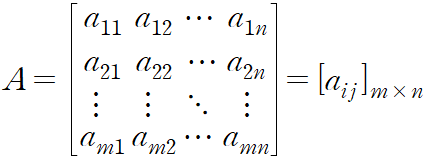
$ m\times 1 $ 행렬은 하나의 열만 있으므로 행벡터(row vector), $ 1\times n $행렬은 하나의 열만 있으므로 열벡터(column vector)라고 하며, 벡터는 보통 굵은 문자 $ \textbf{x, y, z} $등을 이용하여 나타낸다.
- $ A $를 $ n $차 정사각행렬이라고 정의하면,
(1) 성분 $ a_{11}, a_{22}, ..., a_{nn} $은 $ A $의 주대각성분(diagonal entries)이라고 한다.
(2) 주대각성분을 제외한 다른 성분들이 모두 0일때, $ A $를 대각행렬(diagonal matrix)이라고 한다.
(3) 주대각성분 아래(또는 위) 성분들이 모두 0이면, $ A $를 상(또는 하)삼각행렬(upper(또는 lower) triangular matrix)라고 한다. - 행렬 $ A=[a_{ij}]_{m\times n} $에 대하여 행렬 $ A $의 전치행렬(transpose)은 $ A^T $로 나타내고, 다음과 같이 정의한다. $ [A^T]_{ij}=[A]_{ji} $
- 만약 정사각행렬 $ A $가 $ A^T=A $라면 $ A $는 대칭행렬(symmetric matrix), $ A^T=-A $라면 반대칭행렬(skew-symmetric matrix)라고 한다. 아래 그림과 같이 주대각성분을 기준으로 대칭 또는 반대칭이다.

- 행렬의 상수배(scalar multiplication of matrix)
$ m\times n $행렬 $ A=[a_{ij}] $와 상수 $ k $, $ k\in \mathbb{R} $에 대하여, 행렬 $ A $의 $ k $배를 다음과 같이 정의한다. 모든 $ i, j $에 대하여 $ [kA]_{ij}=k[A]_{ij} $

- 행렬의 덧셈(sum of matrices)
두 행렬 $ A=[a_{ij}]_{m\times n}, B=[b_{ij}]_{m\times n} $에 대하여 $ A $와 $ B $의 합을 다음과 같이 정의한다.

$ A+B=[A+B]_{ij}=[A]_{ij}+[B]_{ij} $
두 행렬의 합은 두 행렬의 행과 열의 개수가 서로 같을 때에만 정의된다.
- 행렬의 모든 성분이 0인 행렬을 영행렬(zero matrix)이라고 하며, $ \textbf{0} $로 나타낸다.
- $ A, B, C $가 서로 같은 크기의 행렬이고, $ k, l $은 스칼라라고 하면 다음이 성립한다.
(1) $ A+B=B+A $ (교환법칙)
(2) $ (A+B)+C=A+(B+C) $ (결합법칙)
(3) $ A+\textbf{0}=\textbf{0}+A=A $
(4) $ A+(-A)=(-A)+A=\textbf{0} $
(5) $ k(A+B)=kA+kB $
(6) $ (k+l)A = kA+lA $
(7) $ (kl)A=k(lA) $
(8) $ 1A=A $
(9) $ (kA)^T=kA^T, (A+B)^T=A^T+B^T $ - 행렬의 곱셈(products of matrices)
두 행렬의 곱이 성립하려면 앞 행렬의 열 개수와 뒤 행렬의 행 개수가 같아야 하며 곱한 행렬의 크기는 앞 행렬의 행 개수와 뒤 행렬의 열 개수와 같다. 두 행렬 $ [A_{ij}]_{m\times l}, [B_{ij}]_{l\times n} $에 대하여 행렬 $ A $의 $ i $번째 행벡터를 $ \textbf{a}_{i} $, 행렬 $ B $의 열벡터를 $ \textbf{b}_{j} $라고 하면, 두 행렬의 곱은 다음과 같이 정의한다.
$AB=\begin{bmatrix}
\textbf{a}_{1}\textbf{b}_{1}&\textbf{a}_{1}\textbf{b}_{2} &\cdots &\textbf{a}_{1}\textbf{b}_{n} \\
\textbf{a}_{2}\textbf{b}_{1}&\textbf{a}_{2}\textbf{b}_{2} &\cdots &\textbf{a}_{2}\textbf{b}_{n} \\
\vdots &\vdots &\ddots &\vdots \\
\textbf{a}_{m}\textbf{b}_{1}&\textbf{a}_{2}\textbf{b}_{2} &\cdots &\textbf{a}_{m}\textbf{b}_{n} \\
\end{bmatrix}$
$ [AB]_{ij} = \textbf{a}_{i}\textbf{b}_{j}=a_{i1}b_{1j}+a_{i2}b_{2j}+\cdots+a_{il}b_{lj}=\sum_{k=1}^{l}a_{ik}b_{kj} $
쉽게 풀어쓰면 $ AB $의 $ i $행 $ j $열의 성분은 $ A $의 $ i $번째 행벡터와 $ B $의 $ j $번째 열벡터의 내적이다.
$ AB=\begin{bmatrix}
a_{11} &a_{12} &\cdots &a_{1l} \\
\vdots &\vdots & &\vdots \\
{\color{Red}a_{{\color{Red}i }{\color{Red} 1}}}&{\color{Red}a_{{\color{Red}i }{\color{Red} 2}} }&{\color{Red}\cdots }&{\color{Red}a_{{\color{Red} i}{\color{Red} l}} } \\
\vdots &\vdots & &\vdots \\
a_{m1} &a_{m2} &\cdots &a_{ml} \\
\end{bmatrix}\begin{bmatrix}
b_{11} &\cdots &{\color{Red}b_{{\color{Red} 1}{\color{Red} j}}} &\cdots &b_{1n} \\
b_{21} &\cdots &{\color{Red} b_{{\color{Red} 2}{\color{Red} j}}} &\cdots &b_{2n} \\
\vdots & &{\color{Red}\vdots } & &\vdots \\
b_{l1} &\cdots &{\color{Red}b_{{\color{Red}l}{\color{Red} j}}} &\cdots &b_{ln} \\
\end{bmatrix} $ - 주대각성분이 모두 1이고 나머지 성분들은 모두 0인 $ n $차 행렬을 항등행렬(identity matrix)라고 하며 다음과 같이 나타낸다. $ I_{n}=\begin{bmatrix}
1&0 &\cdots &0 \\
0& 1 & & \vdots \\
\vdots & & \ddots & 0 \\
0 & \cdots & 0 & 1 \\
\end{bmatrix} $ - $ A, B, C $가 행렬의 곱셈이 서로 성립하는 임의의 행렬이라 하고, $ k $를 임의의 스칼라라고 하면 다음이 성립한다.
(1) $ A(BC)=(AB)C $(결합법칙)
(2) $ A $가 $ m\times n $행렬이면 $ I_{m}A=A $이고 $ A=AI_{n} $이다.
(3) $ A(B+C)=AB+AC $이고 $ (A+B)C=AC+BC $ (분배법칙)
(4) $ k(BC)=(kB)C=B(kC) $
(5) $ (AB)^T=B^TA^T $
주의할 점: 행렬에서는 일반적으로 곱셈의 교환법칙이 성립하지 않는다. $ AB\neq BA $
'Mathematics > 선형대수(Linear Algebra)' 카테고리의 다른 글
| Chapter 3-1. 부분 공간과 일차 독립 (0) | 2022.05.26 |
|---|---|
| Chapter 2-2. 여인자 전개와 크래머 공식 (0) | 2022.05.26 |
| Chapter 2-1. 행렬식의 정의와 성질 (0) | 2022.05.24 |
| Chapter 1-3 역행렬과 선형연립방정식의 해 구하기 (0) | 2022.05.24 |
| Chapter 1-1. 선형연립방정식과 Gauss-Jordan 소거법 (0) | 2022.05.24 |