- $ m\times n $ 행렬 $ A $와 $ n \times m $행렬 $ B $에 대하여 $ BA=I_{n} $을 만족하면 , $ B $를 $ A $의 좌역행렬(left inverse)라고 하고, $ AC=I_{m} $을 만족하는 $ n\times m $행렬 $ C $를 $ A $의 우역행렬(right inverse)라고 한다.
만약 $ n\times n $행렬 $ A $가 좌역행렬 $ B $와 우역행렬 $ C $를 가지면 $ B=BI_{n}=B(AC)=(BA)C=I_{n}C=C $이므로 $ B=C$이다.
$ n\times n $행렬 $ A $에 대하여 $ AB=I_{n}=BA $를 만족하는 행렬 $ B $가 존재하면 $ A $는 가역(invertible)이라 하고, $ B $를 $ A $의 역행렬(inverse)라고 하며 $ A^{-1} $로 나타낸다. - 가역행렬 $ A, B $와 스칼라 $ k $에 대하여 다음 성질이 성립한다.
(1) $ (AB)^{-1}=B^{-1}A^{-1} $
(2) $ (kA)^{-1}=\frac{1}{k}A^{-1} $
(3) $ (A^{-1})^{-1}=A $
(4) $ A^{-n}=(A^n)^{-1}=(A^{-1})^n $
(5) $ (A^T)^{-1}=(A^{-1})^T $ - 단위행렬(identity matrix) $ I_{n} $에 기본행 연산 세 가지 중 하나만을 적용하여 얻은 행렬을 기본행렬(elementary matrix)라고 하고, 보통 $ E $로 나타낸다. 단위행렬의 한 행에 상수배를 하거나(type I), 단위행렬의 서로 다른 두 행의 위치를 바꾸거나(type II), 단위행렬의 한 행에 다른 행의 상수배를 더하여 구할 수 있다(type III).

- 임의의 행렬의 왼쪽에 기본행렬을 곱한 결과는 기본행렬에 대응하는 기본행 연산을 주어진 행렬에 시행한 결과와 같다.

- $ A $가 $ n\times n $행렬이라고 할때, 다음 명제들을 동치이다.
(1) $ A $는 가역(invertible)이다.
(2) $ A\textbf{x}=\textbf{0} $은 오직 자명한 해 $ \textbf{x}=\textbf{0} $만을 해로 갖는다.
(3) $ A $와 $ I_{n} $은 행일치(row-equivalent)이다.
(4) $ A $는 기본행렬들의 곱으로 표현할 수 있다. - 삼각행렬이 가역일 필요충분조건은 주대각성분에 0이 없는 것이다.
- 역행렬을 구하는 방법
① $ n $차 정사각행렬 $ A $가 가역(invertible)이면 $ I_{n} $과 행일치이므로 Gauss-Jordan 소거법을 이용하여 다음과 같이 기본행렬들의 곱으로 표현할 수 있다. $ E_{k}\cdots E_{2}E_{1}A=I_{n} $.
② $ I_{n}=A^{-1}A=E_{k}\cdots E_{2}E_{1}A $이므로 $ A^{-1}=E_{k}\cdots E_{2}E_{1} $이다.
예제) $ A=\begin{bmatrix}
1 &1 &1 \\
1 &2 &1 \\
1 &3 &0 \\
\end{bmatrix} $의 역행렬을 구하여라.

주어진 행렬을 왼쪽에, 기본행렬을 오른쪽에 표시한다.
2행에서 1행을 뺀다. $ E_{1}=\begin{bmatrix}
1 &0 &0 \\
-1 &1 &0 \\
0 &0 &1 \\
\end{bmatrix}$

3행에서 1행을 뺀다. $ E_{2}E_{1}=\begin{bmatrix}
1 &0 &0 \\
-1 &1 &0 \\
-1 &0 &1 \\
\end{bmatrix} $
1 &0 &0 \\
-1 &1 &0 \\
-1 &0 &1 \\
\end{bmatrix} $
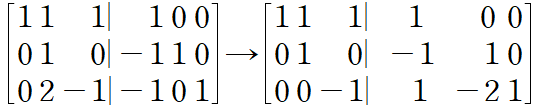
3행에서 2행의 2배를 뺀다. $ E_{3}E_{2}E_{1}=\begin{bmatrix}
1 &0 &0 \\
-1 &1 &0 \\
1 &-2 &1 \\
\end{bmatrix} $
1 &0 &0 \\
-1 &1 &0 \\
1 &-2 &1 \\
\end{bmatrix} $
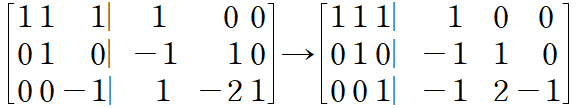
3행에 -1을 곱한다. $ E_{4}E_{3}E_{2}E{1}=\begin{bmatrix}
1 &0 &0 \\
-1 &1 &0 \\
-1 &2 &-1 \\
\end{bmatrix} $
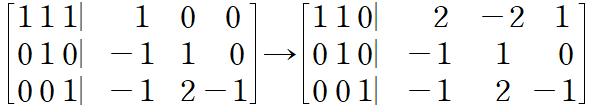
1행에서 3행을 뺀다. $ E_{5}E_{4}E_{3}E_{2}E{1}=\begin{bmatrix}
2 &-2 &1 \\
-1 &1 &0 \\
-1 &2 &-1 \\
\end{bmatrix} $
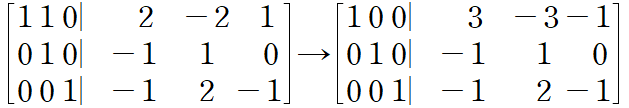
마지막으로, 1행에서 2행을 빼주면 왼쪽에 단위행렬이 완성되고 $ A $의 역행렬을 구할 수 있다.
$ A^{-1}=E_{6}\cdots E_{1}=\begin{bmatrix}
3 &-3 &1 \\
-1 &1 &0 \\
-1 &2 &-1 \\
\end{bmatrix} $
$ A^{-1}=E_{6}\cdots E_{1}=\begin{bmatrix}
3 &-3 &1 \\
-1 &1 &0 \\
-1 &2 &-1 \\
\end{bmatrix} $
- 만약 $ A $가 가역(invertible)인 $ n\times n $ 행렬이면, 어떠한 열벡터(column vector) $ \textbf{b}=[b_{1}\cdots b_{n}]^T $에 대하여 선형연립방정식 $ A\textbf{x}=\textbf{b} $ 가 오직 하나의 해 $ \textbf{x}=A^{-1}\textbf{b} $를 갖는다. 만약 $ A $가 비가역(not invertible)이면 이 연립방정식은 해가 없거나 무수히 많은 해를 갖는다.
'Mathematics > 선형대수(Linear Algebra)' 카테고리의 다른 글
| Chapter 3-1. 부분 공간과 일차 독립 (0) | 2022.05.26 |
|---|---|
| Chapter 2-2. 여인자 전개와 크래머 공식 (0) | 2022.05.26 |
| Chapter 2-1. 행렬식의 정의와 성질 (0) | 2022.05.24 |
| Chapter 1 - 2. 행렬의 덧셈과 곱셈 (0) | 2022.05.24 |
| Chapter 1-1. 선형연립방정식과 Gauss-Jordan 소거법 (0) | 2022.05.24 |